Chenkaixuan's Blog

Embrace The Grind

0%

Stacks And Queues in Data structure

发表于 更新于

1

Basic

Stacks and queues are two special linear lists.
In terms of structure, both are linear lists, but in terms of operation, the basic operations they support are only a subset of linear list operations So they are linear lists with restricted operations.

Stack

Definition:

It is a linear list that allows insertion or deletion only at the end of the list.
The end that allows insertion and deletion is called the top of the stack, and the other side is called the bottom of the stack.

Features

Above gives it a feature : Last In First Out (LIFO)
The latest node added to a stack is the node which is eligible to be removed first.

Stack Data Structure and Implementation in Python, Java and C/C++

basic OP code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/* 初始化栈 */
stack<int> stack;

 /* 元素入栈 */
stack.push(1);

/* 访问栈顶元素 */
    int top = stack.top();

/* 元素出栈 */
    stack.pop(); // 无返回值

/* 获取栈的长度 */
    int size = stack.size();
/* 判断是否为空 */
    bool empty = stack.empty();

stack structure

every element in this stack is a listNode which has this structure

1
2
3
4
5
6
7
8
9
class listNode{
friend class MyStack;
private:
    listNode* next;
    int data;
public:
    listNode();
    listNode(int nodeData, listNode* succ = NULL);
}

The indispensable compositions of a stack are

  1. a top-pointer for keeping track of the most recently added item, the stack’s top pointer allows you to quickly access and manipulate the top element.
  2. stackSize

So we have

1
2
3
4
5
class MyStack
{
private:
    listNode* topNode;
    int stackSize;

Some real shit

洗干净的盘子总是逐个往上叠放在已经洗好的盘子上面，而用时从上往下逐个取用 。

So In programming, if you need to use data in the reverse order of how it was saved, you can use a stack to do it.

括号匹配的检验

假设表达式中允许包含两种括号：圆括号和方括号，其嵌套的顺序随意，即([ ] (）)或[ ([ ] [ ］）］等为正确的格式，［（］或（［（））或（（）］）均为不正确的格式。检验括号是否匹配的方法可用”期待的急迫程度”这个概念来描述 。 例如，考虑下列括号序列：
[ ([ ] [ ]) ] 按从 1-8 编号

当计算机接受了第一个括号后,它期待着与其匹配的第八个括号的出现,然而等来的却是
第二个括号,显然第二个括号的期待急迫性高于第一个括号,此时第一个括号“[”只能暂时靠
边,而迫切等待与第二个括号相匹配的、第七个括号“)”的出现。类似地,因等来的是第三个
括号“[”,其期待匹配的程度较第二个括号更急迫,则第二个括号也只能靠边,让位于第三个
括号。在接受了第四个括号之后,第三个括号的期待得到满足,消解之后,第二个括号的期待
匹配就成为当前最急迫的任务了, …… ,依次类推。可见,这个处理过程恰与栈的特点相吻合。
每读入一个括号,若是右括号,则或者使置于栈顶的最急迫的期待得以消解,或者是不合法的
情况;若是左括号,则作为一个新的更急迫的期待压入栈中,自然使原有的在栈中的所有未消
解的期待的急迫性都降了一级。

Some data structures are Originally recursive

For example ,linklist,

1
2
3
4
5
6
class listNode
{
    friend class linkList;
    friend void merge(linkList &, linkList &);
    float data;
    listNode *next;}

It uses itself inside its definition,

两栈共享空间

两栈共享空间指的是两个栈使用同一个存储数组，而不是各自分配独立的内存空间。在这个设计中，栈 1 从数组的起始位置（V[1]）向上生长，而栈 2 从数组的末尾（V[m]）向下生长

栈满的条件：

  • 如果栈 1 的顶端（top[1]）与栈 2 的底部（top[2]）相遇，说明没有空间可用。
  • 所以，栈满的条件是 top[1] + 1 == top[2]。

Queue

what is Queue?
A queue is a data structure that follows the First-In-First-Out (FIFO) principle. This means that the first element added to the queue will be the first one to be removed. Queues are commonly used in scenarios where order needs to be preserved.

In a queue, you add items at the rear and remove them from the front. This creates a first-in, first-out (FIFO) structure, meaning the first item added is the first one to be removed.

basic op

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
/_ Initialize the queue _/
queue<int> queue;

/_ Add elements to the queue _/
queue.push(1);

/_ Access the front element of the queue _/
int front = queue.front();

/_ Remove the front element from the queue _/
queue.pop(); // No return value

/_ Get the size of the queue _/
int size = queue.size();

/_ Check if the queue is empty _/
bool empty = queue.empty();

senario

In server environments, queues help manage incoming requests, processing them in the order they arrive to maintain fairness. Why fairness? Because the first request that arrives should be the first one to be processed.
I can articulate this by using server-side-code

1
2
3
4
5
6
7
8
9
#include <queue>

void processRequest(std::queue<Request>& requests) {
    while (!requests.empty()) {
        Request request = requests.front();
        requests.pop();
        process(request);
    }
}

implementation

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class MyQueue {
private:
    int* queue;       // Array to hold the queue elements
    int capacity;     // Maximum number of elements the queue can hold
    int front;        // Index of the front element
    int rear;         // Index of the rear element
    int count;        // Current size of the queue

public:
    // Constructor to initialize the queue
    MyQueue(const int& capacity) : capacity(capacity), front(0), rear(-1), count(0) {
        queue = new int[capacity]; // Allocate memory for the queue
    }

    // Destructor to free memory
    ~MyQueue() {
        delete[] queue; // Deallocate the queue array
    }

    // Additional methods like enqueue, dequeue, etc., can be added here
};

顺序循环队列的 rear 是指可以加入元素的索引吗，还是目前队列的最后一个元素的索引 front 呢

  1. **front**：指向队列的第一个元素。 也就是说，这是即将被删除的元素的索引。

  2. rear：指向可以插入元素的位置。也就是说，rear 是下一个要插入元素的索引，指向下一个可用的位置。而不是最后一个元素的索引。

  3. 队列的状态

    • 空队列：front 和 rear 都指向同一个位置，且队列为空。
    • 满队列：rear 的下一个位置是 front，即 (rear + 1) % capacity == front 循环过来的

顺序循环的

队列初始化

假设我们有一个容量为 5 的队列：

1
2
3
4
5
capacity = 5
queue = [_, _, _, _, _]
front = 0
rear = 0
count = 0

空队列状态

在初始化时，队列为空，front 和 rear 都指向位置 0：

1
2
3
4
queue = [_, _, _, _, _]
front = 0
rear = 0
count = 0

插入元素

我们依次插入 4 个元素（10, 20, 30, 40）：

  1. 插入 10：

    1
    2
    3
    4
    queue = [10, _, _, _, _]
    front = 0
    rear = 1
    count = 1

  2. 插入 20

    1
    2
    3
    4
    queue = [10, 20, _, _, _]
    front = 0
    rear = 2
    count = 2

  3. 插入 30

    1
    2
    3
    4
    queue = [10, 20, 30, _, _]
    front = 0
    rear = 3
    count = 3

  4. 插入 40

    1
    2
    3
    4
    queue = [10, 20, 30, 40, _]
    front = 0
    rear = 4
    count = 4

  5. 满队列状态

    再插入一个元素（50），队列将满：

    1
    2
    3
    4
    queue = [10, 20, 30, 40, 50]
    front = 0
    rear = 0  // rear 回到起点
    count = 5

总结

  1. 每次插入一个元素后 rear 都会更新为 (rear + 1) % capacity。

  2. rear 永远不应该等于=capacity 最大值是 capacity-1 应为当 rear 为 capacity-1 的时候就意味着下一个要插入元素的索引，也就是下一个可用的位置是这个数组的最后一个空位了

  3. 更新 front 的位置：在循环中需要移动的元素不需要整个数组移动。你应该直接更新 front 的位置。

    1
    2
    item = queue[front]; // 获取 front 指向的元素
        front = (front + 1) % capacity; // 更新 front 的位置

priority queue

Priority Queue is a linear data structure that has the priority associated with each element. So, the elements are served in the order of highest to lowest priority. If multiple elements have the same priority, they are served as per their original order.

优先级队列是不同于先进先出队列的另一种队列，每次从队列中取出的是具有最高优先权的元素。

在最小优先队列 (min priority queue) 中，查找操作用来搜索优先权最小的元素，删除操作用来删除该元素。最小优先队列，无论入队顺序，当前最小的元素优先出队。
在最大优先队列 (max priority queue) 中，查找操作用来搜索优先权最大的元素，删除操作用来删除该元素。最大优先队列，无论入队顺序，当前最大的元素优先出队。
对于优先权相同的元素，可按先进先出次序处理或按任意优先权进行

优先队列具有最高级先出 (first in, largest out) 的行为特征

双端队列

双端队列是普通队列的扩展，是指允许两端都可以进行入队和出队操作的队列（即可以在队头进行入队和出队操作，也可以在队尾进行入队和出队操作的队列）。其元素的逻辑结构仍然是线性结构，可以采用顺序存储，也可以采用链式存储。将队列的两端分别称为前端和后端，两端都可以入队和出队。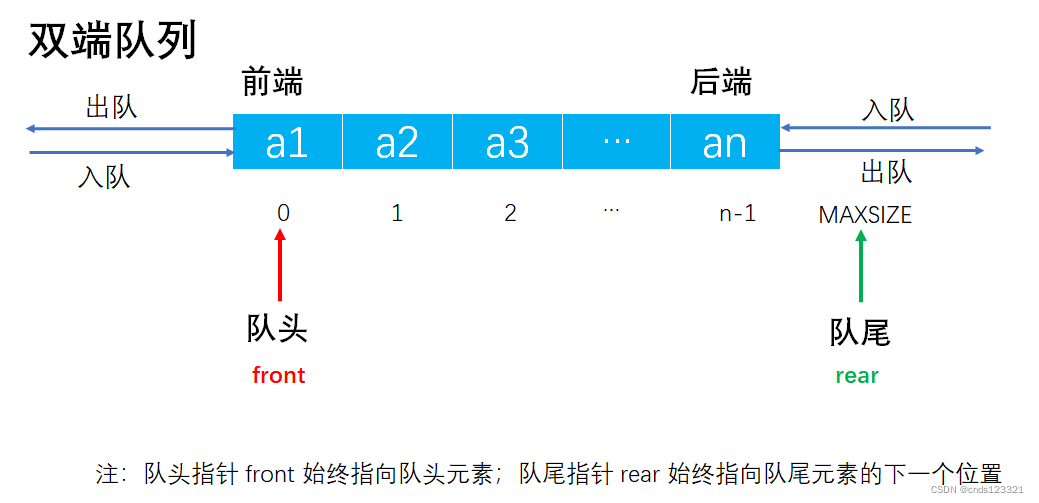

循环对列

循环队列的队头和队尾指针分别为 front 和 rear，则判断循环队列为空的条件是（ ）。
front==rear

基于 MyStack 进行扩展改进

中缀表达式就是我们平时写的数学表达式，比如 3 + 4 * 5。在这个表达式中，运算符（如 + 和 *）位于操作数之间。

后缀表达式（也叫逆波兰表达式）则把运算符放在操作数后面，比如 3 4 5 * +。这种表示法不需要括号，因为运算顺序是通过运算符的位置来决定的。

计算后缀表达式可以用栈来实现

1
2
3
4
5
从左到右遍历后缀表达式的每个元素：
如果是数字，压入栈中。
如果是运算符（如 +、-、*、/），则：
从栈中弹出两个数字（第一个弹出的为右操作数，第二个弹出的为左操作数）。
进行相应的运算，并将结果压回栈中。