Chenkaixuan's Blog

Embrace The Grind

0%

Isolation Forest

发表于 更新于

想象你在一个巨大的仓库里堆满了苹果，但有人偷偷混进了几个烂苹果。你的任务是快速找到这些烂苹果。你会怎么做？

  • 传统方法：检查每个苹果的颜色、形状、气味，然后记住“正常苹果的标准”（比如红色、圆形、香甜）。
    问题是：仓库里有成千上万个苹果，逐个检查需要耗费大量时间。

  • 隔离森林的聪明方法：直接问：“哪个苹果最容易被挑出来？”
    因为烂苹果通常与众不同：比如颜色发黑、形状畸形。它们不需要被详细分析，只需要被快速“隔离”。

Explaination

The method selects a feature and makes a random split in the data between the minimum and the maximum values of that feature.

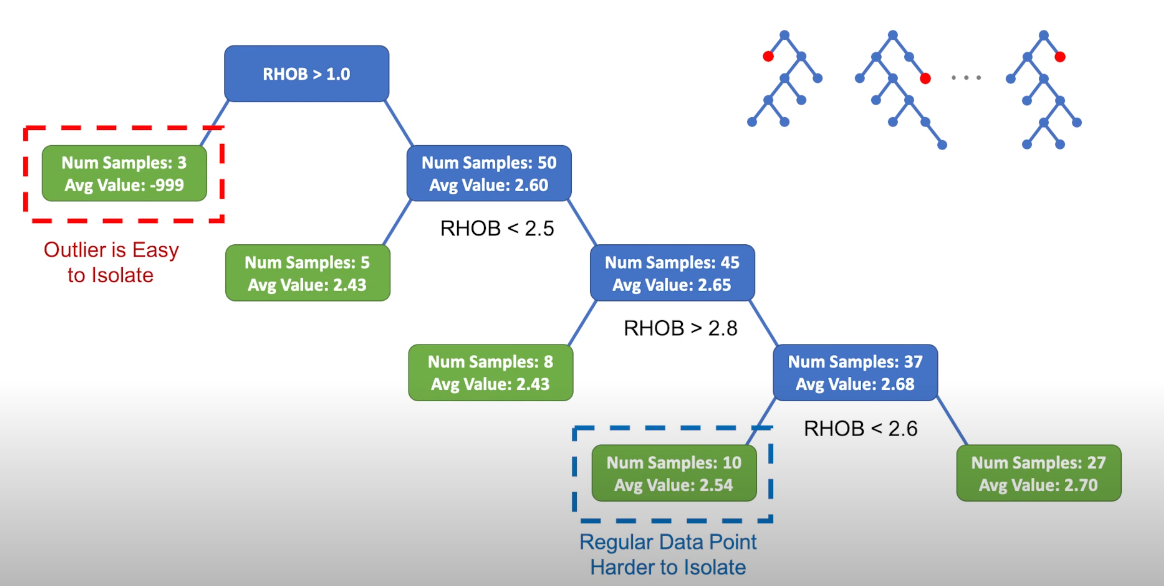
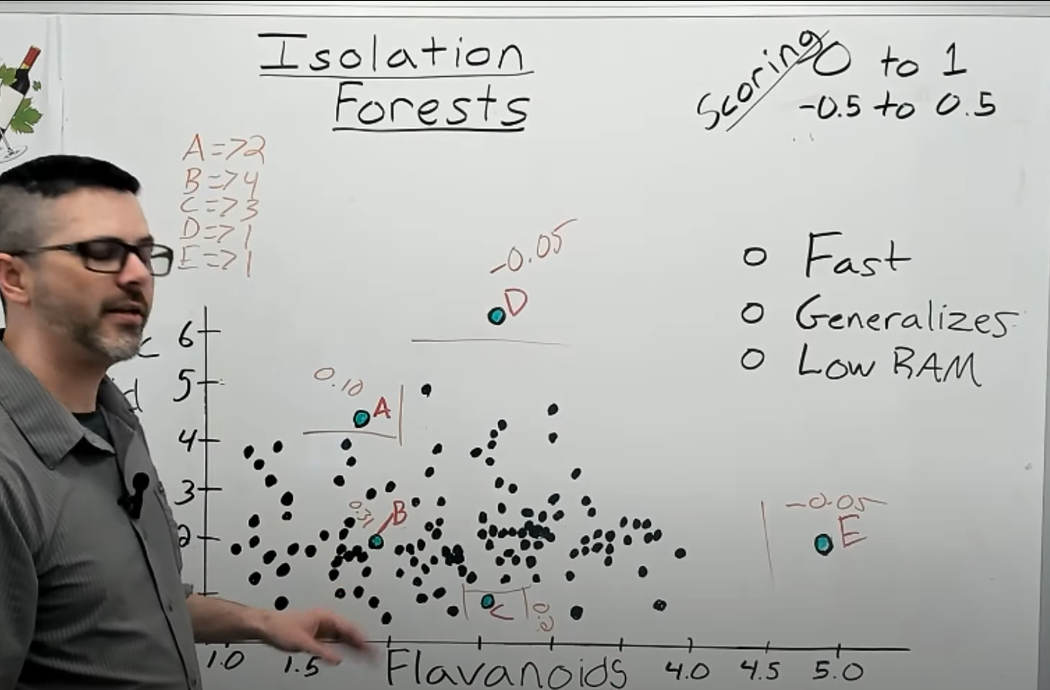
为什么需要隔离森林？

传统方法的问题：
1 需要大量数据去定义“什么是正常”（比如统计平均值）。
2 计算复杂，速度慢（尤其是数据量很大时）。

隔离森林的核心思想

不定义正常，只关注异常

并且

即使数据有成千上万个特征（比如传感器数据），随机选择特征依然有效。

It doesn’t need labels for data(to indicate which one is anomaly),it maps data to a high dimensional space in which the anomaly is far away from the majority-composed space

The ensemble.IsolationForest ‘isolates’ observations by randomly selecting a feature and then randomly selecting a split value between the maximum and minimum values of the selected feature.

Since recursive partitioning can be represented by a tree structure, the number of splittings required to isolate a sample is equivalent to the path length from the root node to the terminating node.

This path length, averaged over a forest of such random trees, is a measure of normality and our decision function.

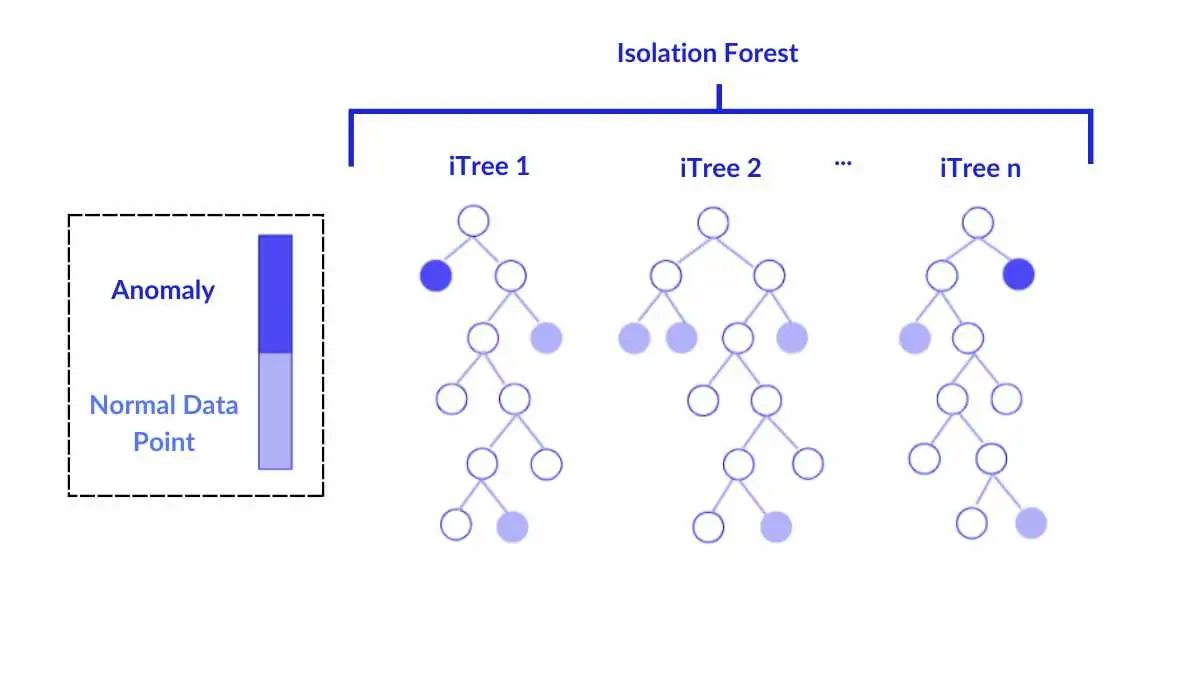
隔离树的构建过程（Isolation Tree）

假设有这样四个特征for a log| 日志等级 | 服务 | 状态码 | 实际含义 

1
2
3
4
5
| 0 (INFO) | 1 (payment) | 200 | 正常支付成功 |
| 0 (INFO) | 1 (payment) | 429 | 正常限流 |
| 1 (WARN) | 1 (payment) | 429 | 正常重试 |
| 0 (INFO) | 2 (database) | 200 | 正常查询 |
| 2 (ERROR)| 0 (auth) | 500 | 异常：认证服务报错 |

步骤1：构建第一棵隔离树

随机选择特征：服务

随机分割值：1.5（介于服务编号1和2之间）

1
2
3
4
         [所有5条数据]
            /   \
服务 ≤1.5(支付类)  服务 >1.5(数据库)
  (4条数据)          (1条数据)

新随机特征：状态码（特征2）

继续分割左子树（4条数据）：

随机分割值：300（介于200-500之间）

1
2
3
4
       [服务 ≤1.5]
          /   \
状态码 ≤300    状态码 >300
 (3条)          (1条)

随机特征：日志等级（特征0）

分割值：0.5（介于INFO和WARN之间）

1
2
3
4
      [状态码 ≤300]
         /   \
等级 ≤0.5   等级 >0.5
 (2条)       (1条)

最终树结构：

1
2
3
4
5
Root(服务≤1.5)
├─ Left(状态码≤300)
│  ├─ Left(等级≤0.5) → 2条
│  └─ Right(等级>0.5) → 1条
└─ Right(服务>1.5) → 1条

步骤2：计算路径长度

  • 异常点（ERROR, auth, 500）：在根节点直接进入右分支 → 路径长度=1

  • 正常点（INFO, payment, 200）：需要经过3次分割 → 路径长度=3

步骤3：构建多棵树（第二棵树）

分割值：450 → 隔离异常点需要2次分割

1
2
3
Root(状态码≤450)
├─ Left → 4条（需要继续分割）
└─ Right → 1条（异常点）

接着继续随机选择

步骤4：综合所有树的结果

假设共5棵树，某个点路径长度分别为：1,2,1,3,1

平均路径长度 = (1+2+1+3+1)/5 = 1.6

步骤5：计算异常得分

$$ s = 2^{-\frac{1.6}{c(5)}} \approx 2^{-1.6/2.1} \approx 0.57 $$

​ $$ c(n) = 2H(n-1) - \frac{2(n-1)}{n} $$

  • $n=5$（样本量）

  • $H(4) = 1 + 1/2 + 1/3 + 1/4 ≈ 2.08$（调和数）

当设定阈值=0.5时：

  • 0.57 > 0.5 → 判定为异常

民主投票：5棵树中4棵认为某点易隔离 → 判定为异常

  • 某点在某棵树中 “易隔离”的数学条件：该样本在树中的路径长度 < 该树的平均路径长度
    即路径长度 < 当前树的平均路径长度 → 视为异常候选

参数解释

contamination=0.05

1
model = IsolationForest(contamination=0.05)
1
未知情况：使用'auto'（默认阈值0.1）

假设有 1000 个样本，得分分布：

1
2
3
4
5
6
7
8
9
10
11
| 得分区间 | 样本数 |

|---------|--------|

| 0.8-1.0 | 50 |

| 0.6-0.8 | 100 |

| 0.4-0.6 | 200 |

| 0.2-0.4 | 650 |

当设置 contamination=0.05：预期每天约 5%的日志需要告警

  • 阈值位置 = 1000 × 0.95 = 950

  • 取第 950 个样本的得分（假设为 0.78）

  • 判定所有得分 ≥0.78 的样本为异常

    根据历史告警比例设置，可通过以下公式估算：

    $$ \text{最佳contamination} = \frac{\text{过去7天平均告警数}}{\text{总日志量}} + 0.02 $$

n_estimators=200

用200棵不同的隔离树进行投票，确保检测稳定性
可能：

1
2
3
4
5
| 树数量 | 检测准确率（模拟数据） | 训练时间（秒） |
|-------|----------------------|---------------|
| 50 | 92% | 0.8 |
| 200 | 98% | 3.2 |
| 500 | 99% | 8.1 |

增加到300-500可提升1-2%准确率，但需测试训练时间是否可接受

max_samples=256

每棵树随机使用256条数据训练

  • 单棵树内存占用：256条 × 3特征 × 4字节 = 3KB
  • 200棵树总内存：200 × 3KB = 600KB

当特征数超过10时，建议保持256；特征较少时可降至128

n_jobs=-1

并行训练多棵隔离树，利用多核CPU加速

random_state=42

固定随机种子，确保每次训练结果一致

计算机使用伪随机数生成器（PRNG）产生随机数

假设构建两棵树：

1
2
3
4
| 运行次数 | 随机数序列     | 特征选择 | 分割值选择 |
| -------- | -------------- | -------- | ---------- |
| 第一次   | 42→12345→67890 | 特征 1   | 0.5        |
| 第二次   | 42→12345→67890 | 特征 1   | 0.5        |